
Professor: When the three planets are in eclipse, the black hole like a door is open. Evil comes, spreading terror and chaos.
See the snake, Billy: the ultimate evil. Make sure you get the snake.
Billy: [drawing] Yes, I've got your snakes. I've got all the snakes.
So when is this snake act supposed to occur?
Professor: Huh? Well, uh ... if this is the five, and this is the one ... [calculates] ... every 5,000 years.
Billy: So ... I've got some time then.
— The Fifth Element
Alpha Male over at AllAboutAlpha.com posted an interesting article yesterday about the concept of kurtosis, or "fat tails," as they relate to hedge fund returns. In it, he debunks the notion that having a fat tailed return distribution necessarily makes a particular investment "riskier" than one with a more "normal" or even thin-tailed distribution. (Normal distributions by definition have kurtosis—or "excess kurtosis"—of zero.)
In the way normal humans understand and talk about risk, a "riskier" investment is clearly understood by all to mean one that has a higher probability of a loss of a given size than another investment. We need not resort to a discussion about fat tails to understand that this depends on the return variance (σ2)—or, the related concept of standard deviation, or volatility (σ)—of the investment in question. Take, for example, a gander at the following normal Gaussian distributions (remember: kurtosis = 0 for all of these):
With the exception of the squirrelly distribution plot with the purple line (where the mean, or average (μ), equals –2)—which you should ignore—all of these normal distributions have the same mean and the same cumulative probability distribution function. They all just have different variances (red = 0.2, green = 1.0, blue = 5.0). Believe it or not, none of them have "fat tails."
Now, even an idiot—are you listening, Frank Willicott?—can see that the cumulative probability of suffering a "loss" of –1.0 or more (the area under each curve bounded by –1.0 on the right and negative infinity on the left) is substantially different among the different curves: pretty small for the red curve, bigger for the green curve, and pretty scary for the blue curve. Absolute realized returns follow a distribution pattern dictated by the volatility.
So, you can imagine a "fat-tailed" return distribution (where the probability under the "peak" of each normal curve is squooshed further out into the tails, thereby "fattening" them) will indeed have a higher probability of a loss of given amount than a normal curve of identical variance. You can also imagine that a curve with positive excess kurtosis but a standard deviation of 0.45 (σ2 = 0.2)—a "flattened" red curve, if you will—might have a lower cumulative probability of loss of –1.0 or more than the green curve, with σ2 = 1.0. (Although the advantage could dissipate pretty quickly if the kurtosis is high enough.)
This is what Alpha Male was trying to get to, and I think we can all agree with him that we have to pay careful attention to volatility when we are evaluating the riskiness of an investment. Pace Mr. Male, however, we cannot ignore kurtosis, either. So much for the arithmetic.
Unfortunately, the rest of his post is pure sophistry.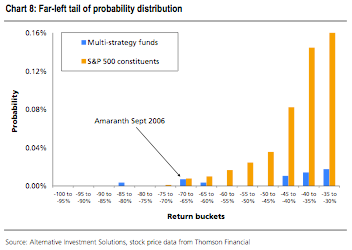
Mr. Male cites at length a presentation made at a recent hedge fund industry confab by Alexander Ineichen of UBS. (Loyal readers know that UBS does not rank high in TED's honor roll at present.) In it ("Food for thought: 2. Loss potential"), Mr. Ineichen trots out a chart (shown above) based on monthly return data between January 1990 and September 2006 for "multi-strategy" hedge funds compared to returns for the individual stock components of the S&P 500. Retrospectively analyzing this data, the crack UBS team comes up with the following:
How do we read the graph? The arrow in the graph points to two occurrences where a multi-strategy fund lost between 65% and 70% of its value in one month. One of these two occurrences was Amaranth’s September 2006 return of -69.8%. (The other occurrence as well as the one observation in the -80% to -85% return bucket was from an obscure fund that we believe managed less than one million in assets and closed in November 1996.) Given that the graph is based on 28,420 monthly multi-strategy returns, we can back out a probability of 0.007% for the probability of a monthly loss in the -65% to -70% return bucket. This is, by coincidence, nearly identical to one of the 500 constituents in the S&P 500 experiencing such a loss in a given month.
More relevant than the probability in a given bucket is the probability of a loss exceeding a certain threshold. For the sake of argument, we examined the probability of a monthly loss exceeding 50%. In the case of multi-strategy funds, there were four occurrences exceeding 50%. This means the probability is in the neighborhood of 0.0141%. What does that mean practically?
This means that if we assume we only invest in one multi-strategy fund for one month we can expect a monthly loss of 50% or more every 7,105 months, i.e., once every 592 years. ...
How do these probabilities compare to the stock market? The probability of losing 50% or more with a S&P 500 constituent is 0.0600%. This means, if we assume we only hold one S&P 500 constituent for one month, we can expect to lose 50% or more once every 139 years. (Note that the probability of losing 50% or more over three, six or twelve months is an entirely different story.)
Well, Mr. Ineichen, thanks for that last little qualification, but I have to say the rest of your analysis is just crap.
First, observed event frequency ex post is not the same thing as expected probability ex ante. Taking historical performance to be a reliable indicator of future behavior is a predictive assumption—one you clearly admit to, for sure—but one I would characterize as pretty near heroic, based upon a data set of four outlier observations over 17 years. You are confident, are you, that an investor in multi-strategy hedge funds could expect a monthly loss of 50% or more once every 592 years? Not 591? Or 593?
Second, even though you do not share it, I have a problem or two with your data. For one thing, where is Long-Term Capital Management, which lost $4 billion in 1998? Gee, I thought LTCM was a "multi-strategy" fund. Was I wrong? (And, even if I am wrong, why the hell would you put up an analysis purporting to describe the loss history of hedge funds since 1990 without making sure to include LTCM?) Furthermore, notwithstanding the fact that you admit not recognizing many of the hedge funds in your database, you are "comfortable," are you, that your "data is of high quality and reasonably complete"? No gaps from selective reporting, especially by—let's say—hedge funds which happened to blow up a month or two after they stopped reporting returns data?
Third, you compare the returns history for multi-strategy hedge funds with individual stocks in the S&P? Are you fucking kidding me? What's the matter: couldn't you find data for the monthly returns of a diversified basket of stocks—say, for example, the S&P 500? I know: let's do a companion study to yours, in which we analyze monthly returns data for diversified long-only equity mutual funds compared to the performance of individual pork belly futures on the Chicago Board of Trade. Ya think that'll provide a balancing perspective?
I am sure the hedge fund audience in Greenwich—UBS's current and potential prime brokerage clients—really ate up your concluding remarks:
Former Harvard president Derek Bok was once quoted saying:"If you think education is expensive, try ignorance."By examining the graph above, could not one rephrase the quote to:"If you think hedge funds are risky, try stocks."
No, sorry, one could not.
This type of article does not even come close to addressing—on a serious, sustained level that does not treat its lay readers as utter morons—the legitimate concerns which investors, regulators, and policy makers outside the hedge fund industry have about its stability, risk controls, and ability to weather unexpected exogenous shocks. (And we're not concerned that you might lose your 34,000 square foot mansion in Greenwich to foreclosure and never get sex again from someone half your age—we're worried about what one of you blowing up is going to do to the rest of us.)
I have a general suggestion for the gentlemen (and ladies?) of the hedge fund industry if you want to seriously play in the marketplace for ideas:
Up your game.
© 2007 The Epicurean Dealmaker. All rights reserved.
